Tugas 7 Lingga 1903015140 Boolean dan Karnaugh Map

Boolean and Karnaugh Map

    Peta Karnaugh adalah alat yang sangat berguna untuk penyederhanaan ekspresi Boolean dalam elektronik digital. Nama lain dari peta Karnaugh adalah K-map atau K map. Ini dapat mewakili persamaan Boolean baik dalam bentuk jumlah produk (sum of products/SOP) dan hasil kali jumlah (product of sum/POS). Ada dua cara untuk menyederhanakan ekspresi Boolean. Salah satunya adalah dengan menggunakan hukum aljabar Boolean dan teorema de Morgan dan yang lainnya adalah dengan menggunakan peta K.

Apa itu peta Karnaugh (k-map)?

    Karnaugh map atau K-map adalah metode bergambar untuk menyederhanakan fungsi atau ekspresi Boolean dalam elektronika digital tanpa menggunakan aljabar Boolean. Pada tahun 1953, fisikawan Amerika Maurice Karnaugh memperkenalkan metode ini. Ini adalah cara termudah untuk mengurangi fungsi logika apa pun ke bentuk sederhana.

Dalam banyak sirkuit digital dan masalah praktis kita perlu menemukan ekspresi dengan variabel minimum. Kita dapat meminimalkan ekspresi Boolean dari 3, 4 variabel dengan sangat mudah menggunakan K-map tanpa menggunakan teorema aljabar Boolean. K-map dapat berbentuk Sum of Product (SOP) dan Product of Sum (POS) sesuai dengan kebutuhan permasalahan. K-map adalah representasi seperti tabel tetapi memberikan lebih banyak informasi daripada TABEL KEBENARAN. Isi dari grid K-map antara 0 dan 1 kemudian menyelesaikannya dengan membuat grup.

Bagaimana cara menyederhanakan peta Karnaugh?

    Semua persamaan Boolean dengan dua atau lebih variabel dapat dengan mudah disederhanakan dengan menggunakan K-maps. Di sini, metode pengelompokan atau metode pemetaan digunakan dengan biner 1 dalam tabel kebenaran ekspresi Boolean. Terdapat aturan dalam menggunakan peta Karnaugh.

Aturan untuk K-Map

1. Pertama menggambar sel tabel kebenaran yang sesuai dengan ekspresi Boolean yang diberikan. Anda harus memperhatikan jumlah variabel. Jumlah sel dalam tabel kebenaran tergantung pada jumlah variabel. Jika n adalah jumlah variabel maka jumlah sel akan menjadi 2n. Tapi ingat, jumlah baris harus kurang dari atau sama dengan jumlah kolom. Misalnya: Dalam 2 variabel K-map, jumlah sel akan menjadi 4. Akan ada 2 baris dan 2 kolom. Dalam K-map dengan 3 variabel, jumlah baris akan menjadi 2 dan jumlah kolom akan menjadi 4.


2. Setelah menggambar sel, kita perlu mengembangkan tabel kebenaran dengan meletakkan 1 di semua sel yang mungkin menurut persamaan Boolean yang diberikan.


3. Gunakan pemetaan atau pengelompokan dengan tetangga 1. Pengelompokan harus dilakukan dengan 8, 4 atau 2 tetangga 1 (mana yang lebih besar). Jika hanya ada satu 1, akan ada grup hanya dengan 1 ini.


4. Ambil variabel umum pada baris dan kolom dari setiap kelompok 1 dan tulis variabel-variabel tersebut dalam bentuk perkalian. Sekarang, ambil jumlah setiap produk variabel dari grup.


5. Lalu bentuk akhir yang disederhanakan dari ekspresi Boolean itu akan terlihat.

Langkah-langkah untuk menyelesaikan ekspresi menggunakan K-map

1. Pilih K-map sesuai dengan jumlah variabel.


2. Identifikasi minterms atau maxterms seperti yang diberikan dalam masalah.


3. Untuk SOP letakkan 1 di blok K-map masing-masing ke minterms (0 di tempat lain).


4. Untuk POS, letakkan 0 di blok K-map masing-masing ke maxterms(1 di tempat lain).


5. Buat grup persegi panjang yang berisi jumlah suku pangkat dua seperti 2,4,8 ..(kecuali 1) dan cobalah untuk mencakup elemen sebanyak mungkin dalam satu grup.


6. Dari kelompok yang dibuat pada langkah 5 temukan istilah produk dan jumlahkan untuk formulir SOP.

BENTUK SOP :

1. K-map dari 3 variabel –

Z= ∑A,B,C(1,3,6,7)

Dari grup merah kita mendapatkan suku produk—

A'C

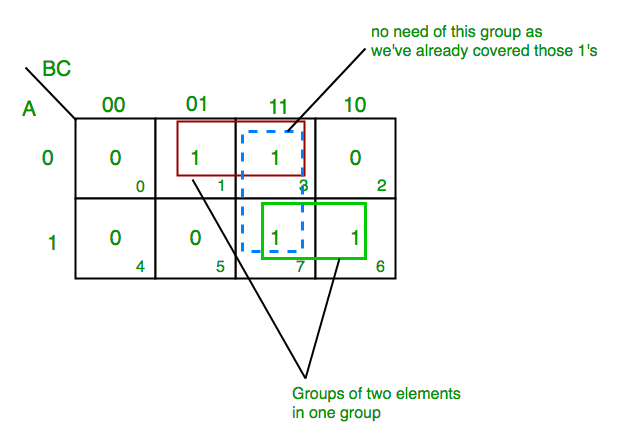
Dari grup hijau kita mendapatkan suku produk—

AB

Menjumlahkan istilah produk ini kita mendapatkan- Ekspresi akhir (A'C+AB)

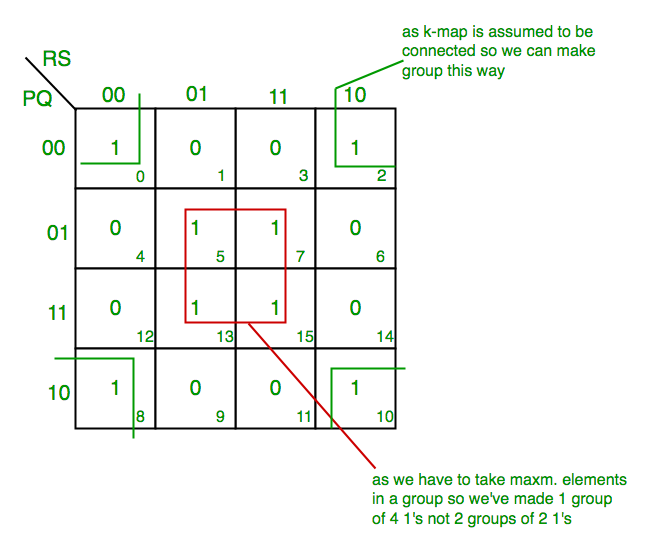
2. K-map untuk 4 variabel –

F(P,Q,R,S)=∑(0,2,5,7,8,10,13,15)

Dari grup merah kita mendapatkan suku produk—

QS

Dari grup hijau kita mendapatkan suku produk—

Q'S'

Menjumlahkan suku produk ini kita mendapatkan- Ekspresi akhir (QS+Q’S’)

BENTUK POS :

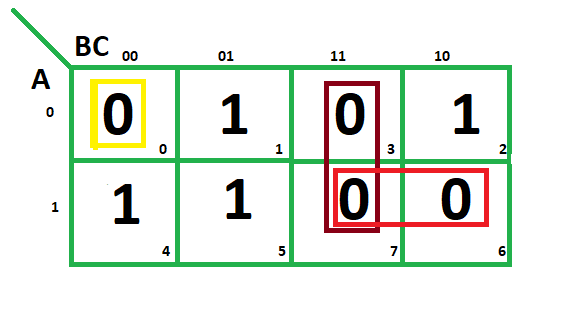
1. K-map dari 3 variabel –

F(A,B,C)=π(0,3,6,7)

Dari grup merah kita menemukan suku 

A     B   

Mengambil pelengkap/complement dari keduanya

A'     B'  

Jumlahkan mereka

(A' + B')

Dari grup coklat kita menemukan suku 

B     C

Mengambil pelengkap/complement dari kedua suku tersebut

B’     C’ 

Jumlahkan mereka

(B’+C’) 

Dari grup kuning kita menemukan suku 

A'     B'     C’ 

Mengambil pelengkap/complement dari keduanya

A     B     C 

Jumlahkan mereka

(A + B + C)

Kita akan mengambil produk dari tiga Suku ini: Ekspresi akhir –

(A' + B') (B' + C') (A + B + C)

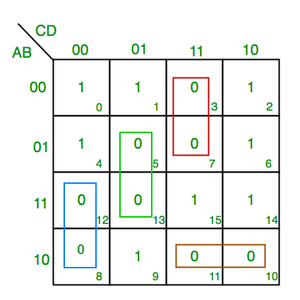
2. K-map untuk 4 variabel –

F(A,B,C,D)=π(3,5,7,8,10,11,12,13) 

Dari grup Hijau kita menemukan suku 

C’     D     B 

Mengambil pelengkap/complement mereka dan menjumlahkannya

(C+D’+B’)

Dari grup merah kita menemukan suku 

C     D     A’ 

Mengambil pelengkap/complement mereka dan menjumlahkannya

(C’+D’+A)

Dari grup Biru kita menemukan suku 

A     C’     D’ 

Mengambil pelengkap/complement mereka dan menjumlahkannya

(A’+C+D) 

Dari grup coklat kita menemukan suku 

A  B’  C 

Mengambil pelengkap/complement mereka dan menjumlahkannya

(A’+B+C’) 

Ekspresi akhir – (C+D’+B’).(C’+D’+A).(A’+C+D).(A’+B+C’) 

*Always remember POS ≠ (SOP)’ 

*The correct form is (POS of F)=(SOP of F’)’ 

Contoh Soal & Jawaban: 

1. K-map digunakan untuk _______

a) minimisasi logika

b) maksimalisasi ekspresi

c) penjumlahan bit paritas

d) pembuatan gerbang logika

Jawaban: A.

2. Sederhanakan ekspresi menggunakan K-maps: F(A,B,C,D)=Σ (1,3,5,6,7,11,13,14).

a) AB+BC’D+A’B’C

b) BCD’+A’C’D+BD’

c) A’D+BCD+A’BC+AB’C’

d) AC’D’+BC+A’BD+C’D’

Jawaban: C.

3. Saat merancang sirkuit untuk meniru tabel kebenaran, ekspresi Product-of-Sums (POS) dan ekspresi Sum-of-Products (SOP) dapat diturunkan dari?

a) k-map

b) NAND gate

c) NOR gate

d) X-NOR gate

Jawaban: A.

4. Sederhanakan ekspresi menggunakan K-maps: F(A,B,C) = (1,3,5,6,7).

a) AC’+B’

b) AB+C

c) AB’+B’C’

d) A’BC+B’C+AC

Jawaban: B.

5. Sederhanakan ekspresi menggunakan K-maps: F(A,B,C) = (0,2,4,5,7).

a) (x+y)(y+z)(x+z)(x’+z’)

b) (x+z’)(y+z)(x+y)

c) (x+y’+z)(x+z’)

d) (y’+z’)(x’+y)(z+y’)

Jawaban: A.

6. Gunakan peta Karnaugh untuk menemukan ekspresi fungsi yang disederhanakan: F = x’yz + xy + xy’z’.

a) xz’+y’z’

b) xy’z+xy

c) y’z+x’y+z

d) yz+xy+xy’z

Jawaban: D.

7. Siapa yang menemukan K-map?

a) Maurice Karnaugh

b) Edward Veitch

c) George Boole

d) Adam Smith

Jawaban: A.

8. Ekspresi yang disederhanakan untuk mengikuti fungsi Boolean F(A, B, C, D) = (0, 1, 2, 3, 6, 12, 13, 14, 15) adalah

(A) A'B' + AB + A'C'D'

(B) A'B' + AB + A'CD'

(C) A'B' + AB + BC'D'

(D) A'B' + AB + BCD'

a) (A) saja

b) (B) saja

c) (A) dan (B) saja

d) (B) dan (D) saja

Jawaban: D.

9. Sebuah K-map dari 3 variabel berisi _______ sel.

a) 8

b) 3

c) 6

d) 9

Jawaban: A.

10. Sebuah K-map dari 4 variabel berisi _______ sel.

a) 12

b) 16

c) 18

d) 8

Jawaban: B.

Sumber: 

    > https://onlinelearning.uhamka.ac.id

    > https://electronicsphysics.com/karnaugh-map/

    > https://www.geeksforgeeks.org/introduction-of-k-map-karnaugh-map/

    > https://engineeringinterviewquestions.com/mcqs-on-boolean-algebra-karnaugh-maps-answers/

    > https://www.sanfoundry.com/discrete-mathematics-questions-answers-karnaugh-maps/

    > https://testbook.com/objective-questions/mcq-on-karnaugh-maps--5eea6a0d39140f30f369e202

    > https://engineeringinterviewquestions.com/mcqs-on-karnaugh-map-answers/