Tugas 6 Lingga 1903015140 Teorema DeMorgan's
De-Morgan's Theorem
- Negasi dari disjungsi adalah konjungsi dari negasi
- Negasi dari konjungsi adalah disjungsi dari negasi
- Komplemen gabungan dua himpunan sama dengan perpotongan komplemennya
- Komplemen perpotongan dua himpunan sama dengan gabungan komplemennya
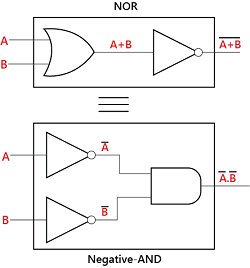
- not (A or B) = (not A) and (not B)
- not (A and B) = (not A) or (not B),
di mana
dan
dimana
| Input variables | Output Condition | ||||
|---|---|---|---|---|---|
| A | B | AND | NAND | OR | NOR |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
0 |
De-Morgan's First Theorem
| Inputs | Output For Each Term | |||||
|---|---|---|---|---|---|---|
| A | B | A.B | (A.B)' | A' | B' | A'A+B' |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
De-Morgan's Second Theorem
| Inputs | Output For Each Term | |||||
|---|---|---|---|---|---|---|
| A | B | A+B | (A+B)' | A' | B' | A'.B' |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
0 |
Example 1: (A.B.C)'
(A.B.C)'=A'+B'+C'
Example 2: (A+B+C)'
(A+B+C)'=A'.B'.C
Example 3: ((A+BC')'+D(E+F')')'
Untuk menerapkan teorema DeMorgan pada bentuk ini, kita harus mengikuti bentuk berikut:
1) Dalam bentuk lengkap, pertama, kita temukan suku-suku di mana kita dapat menerapkan teorema DeMorgan dan memperlakukan setiap suku sebagai variabel tunggal.
Jadi,
2) Selanjutnya, kita terapkan teorema pertama DeMorgan. Jadilah,
3) Selanjutnya, kami menggunakan aturan nomor 9, yaitu, (A=(A')') untuk membatalkan bar ganda.4) Selanjutnya, kita terapkan teorema kedua DeMorgan. Jadi,
5) Sekali lagi terapkan aturan nomor 9 untuk membatalkan bar ganda.
Example 3: (AB'.(A + C))'+ A'B.(A + B + C')'
Contoh Soal & jawaban:
Sumber:
> https://onlinelearning.uhamka.ac.id
> https://www.javatpoint.com/de-morgans-theorem-of-boolean-algebra-in-digital-electronics
> https://en.wikipedia.org/wiki/De_Morgan%27s_laws
> https://www.careerride.com/view/universal-gates-de-morgans-theorem-mcqs-with-answers-
22495.aspx
> https://testbook.com/objective-questions/mcq-on-demorgans-theorem--5eea6a0d39140f30f369e1f4
> https://www.studocu.com/row/document/aljamaa%D8%A9-aleslamy%D8%A9/logical-
design/mcqs-chapter-3-multiple-choice-questions-for-gate-level-minimization/11354840
> https://engineeringinterviewquestions.com/mcqs-on-boolean-algebra-answers/
> https://engineeringinterviewquestions.com/mcqs-on-boolean-logic-operations-answers/
> https://mcq.electronics-club.com/boolean-algebra-mcq/
> https://testbook.com/objective-questions/mcq-on-boolean-algebra--5eea6a1439140f30f369f286













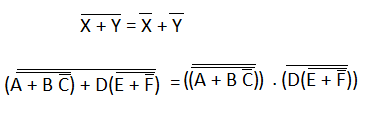
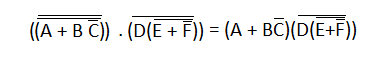
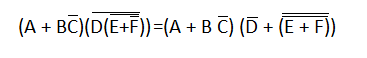

Comments
Post a Comment